Elektroakustik

2002-07-10 15:33

Något lite om delningsfilter

Svante Granqvist 1991-2002

Något lite om delningsfilter

Ett högtalarsystem har oftast fler högtalarelement än ett, eftersom det är svårt att göra ett högtalarelement som klarar att återge hela det hörbara frekvensområdet. För att varje element i ett sådant system ska återge rätt del av frekvensområdet behövs ett delningsfilter. I ett tvåvägssystem med en bashögtalare och en diskanthögtalare ska delningsfiltret se till att basen kommer till bashögtalaren och diskanten kommer till diskanthögtalaren. Signalerna som kommer ut från de två högtalarna summeras sedan akustiskt till någonting som mer eller mindre liknar orginalsignalen. Det finns dock ett flertal saker som kan gå fel på vägen.

· Vid den akustiska summeringen av signalerna från de två högtalarna kan det bli olika löptid fram till lyssnaren. Om högtalarnas akustiska centrum inte sitter nära varandra i förhållande till våglängden kring delningsfrekvensen så kommer det att bli frekvensgångspåverkan i de flesta riktningarna.

· De två högtalarelementen ska ha rak frekvensgång. I första hand gäller det inom de frekvensområden de är avsedda för, men det gäller även en bit utanför dessa, eftersom delningsfiltren inte är oändligt branta.

· Summan av överföringsfunktionerna för de två grenarna i delningsfiltret ska helst bli 1, dvs både amplitud och fas bör lämnas opåverkade.

De två första punkterna får oss att inse några fördelar med branta delningsfilter. Vidare kan de spela in i designen av delningsfiltren såtillvida att man försöker kompensera fas eller amplitudsvar för högtalarelement eller placering. De två första punkterna kommer vi dock inte att behandla vidare här, däremot ska vi behandla den sista lite närmare. Om vi försummar inverkan enligt de två första punkterna och förenklar problemet till att gälla överföringsfunktionen från insignal till summan av de två signalerna ut från delningsfiltret kan vi studera själva filtrens påverkan. Vi ska här undersöka tre delningsfilter av 1:a, 2:a resp 3:e ordningen, för att se vilken påverkan sådana kan ha på amplitud- och fasgång. Vi kommer att göra det på normerad form, den som så önskar kan ersätta s med s/s₀.

1:a ordningens delningsfilter

Lågpassgrenen i ett första ordningens delningsfilter har en pol på reella axeln i s‑planet (ekv. 1). Högpassgrenen har en pol på samma ställe, och dessutom ett nollställe i origo (ekv. 2).

(1) (2)

Överföringsfunktionerna kan antingen adderas (om högtalarelementen fasas lika) eller subtraheras (om den ena högtalaren fasvänds). Detta ger två typfall.

(3) (4)

Adderade signaler (ekv. 3), överföringsfunktionen får en pol och ett nollställe på samma ställe reella axeln som alltså tar ut varandra. Alltså ingen påverkan av signalen.

Subtraherade signaler (ekv. 4), överföringsfunktionen får en pol på samma ställe som de båda grenarna i filtret och ett nollställe speglat i imaginära axeln. Detta filter har inga fördelar jämfört med det första filtret, men är av principiellt intressant eftersom det är av allpasskaraktär, dvs det har ingen påverkan på amplitudsvaret, men fasinformationen blir förvrängd.

Ytterligare en observation vi kan göra är att fasskillnaden mellan två grenarna alltid är 90°, vid alla frekvenser. Vid delningsfrekvensen, när signalerna är lika starka ska amplituden på överföringsfunktionerna därför vara eller –3 dB för att summaamplituden av dem ska bli 1. Så är också fallet.

2:a ordningens delningsfilter

Lågpassgrenen i ett andra ordingens delningsfilter har två poler på reella axeln i s‑planet (ekv. 5). Högpassgrenen har också två poler på samma ställe och dessutom två nollställen i origo (ekv. 6).

(5) (6)

På samma sätt som med först ordningens filter kan överföringsfunktionerna antingen adderas (om högtalarelementen fasas lika) eller subtraheras (om den ena högtalaren fasvänds). Detta ger två typfall.

(7) (8)

Adderade signaler (ekv. 7), överföringsfunktionen får två poler på reella axeln på samma ställe som grenarna i filtret och två poler på imaginära axeln. Detta filter kan inte rekommenderas eftersom det ger en "dip" i amplitudsvaret vid delningsfrekvensen.

Subtraherade signaler(ekv. 8), överföringsfunktionen får två poler på samma ställe som de båda grenarna i filtret, varav en tas ut av ett nollställe. Dessutom får man ett nollställe på positiva reella axeln speglat i imaginära axeln. Kvar blir samma typ av allpassfilter som var möjligt med 1:a ordningens filter. Inget av dessa två fall gav bibehållen fasinformation, men den ena (ekv. 8) gav rakt amplitudsvar pga allpasskaraktären.

Man kan notera att fasskillnaden mellan filtergrenarna 0° i fallet när ena högtalaren fasvänds, vid alla frekvenser. Av denna anledning skall amplituden på överföringsfunktionerna vara 1/2, eller –6 dB vid delningfrekvensen. Man bör alltså inte använda butterworthdimensionering för andra ordningens delningsfilter, eftersom sådana dämpar –3 dB vid delningsfrekvensen. Detta skulle ge en amplitudökning kring delningsfrekvensen.

3:e ordningens delningsfilter

Lågpassgrenen i ett tredje ordingens delningsfilter är av butterworthtyp och har en pol på reella axeln och ett polpar på enhetscirkeln ute i s‑planet (ekv. 9). Högpassgrenen har samma poler som lågpassgrenen och dessutom tre nollställen i origo (ekv. 10).

(9) (10)

Även nu kan överföringsfunktionerna antingen adderas (om högtalarelementen fasas lika) eller subtraheras (om den ena högtalaren fasvänds). De två typfallen blir:

(11) (12)

Adderade signaler (ekv. 11), överföringsfunktionen får tre poler på samma ställe som grenarna i filtret men den på reella axeln tas ut av ett nollställe. Kvar blir två poler ute i det komplexa planet och två nollställen speglade i imaginära axeln. Totalt alltså en allpasskaraktär men av annan typ än tidigare.

Subtraherade signaler (ekv. 12), överföringsfunktionen får tre poler på samma ställe som de båda grenarna i filtret, varav de två ute i komplexa planet tas ut av nollställen. Polen på reella axeln finns kvar och likaså ett nollställe speglat i imaginära axeln, dvs det blir samma allpasskaraktär som för 1:a och 2:a ordningens filter.

I detta fall är fasskillnaden mellan de två grenarna alltid 270°, vid alla frekvenser. Vid delningsfrekvensen, när signalerna är lika starka ska amplituden på överföringsfunktionerna därför vara eller –3 dB för att summaamplituden av dem ska bli 1. Så är också fallet eftersom filtren är butterworthdimensionerade.

n:te ordningens delningsfilter

Vi kan generalisera ovanstående resonemang till att gälla fler delningsfilter:

(13) (14)

Vi behåller i och med detta begränsningarna att P_n(s) är lika i de båda grenarna, och att brantheten i spärrbandet för de båda filtergrenarna är densamma. Under dessa förutsättningarna blir summa-, resp skillnadssignalerna

(15) (16)

Polynomen i täljarna på ekv. 15 och 16 har nollställen som är ”jämnt utspridda” över enhetscirkeln. För att undvika fas- och amplitudpåverkan, måste dessa nollställen tas ut av motsvarande poler via P_n(s). Eftersom åtminstone ett nollställe hamnar i höger halvplan eller på jw-axeln för n³2, kan dessa nollställen inte elimineras med motsvarande poler om filtren ska vara stabila. Däremot kan man spegla dem i jw‑axeln och då blir amplitudsvaret blir rakt, medan fasen fortfarande påverkas. Resultatet blir en allpassfilterfunktion. P_n(s) ska vara ett butterworthpolynom, B_n(s) för udda n och ett kvadratiskt butterworth för jämna n, dvs P_n(s)=[B_n/2(s)]² (Sådana polynom kallas ibland Linkwitz-Riley eller bara Linkwitz). Eftersom fasskillnaden mellan utsignalerna från de olika grenarna blir n×90° (vid alla frekvenser, men speciellt vid delningsfrekvensen) gäller att:

· För udda n kan ena högtalaren polvändas utan att amplitudsvaret ändras

· För n=2,6,10,14… ska ena högtalaren polvändas

· För n=4,8,12,16… ska högtalarna fasas lika.

Allpassfilter?

Vi har sett att både 1:a, 2:a och 3:e ordningens delningsfilter kan uppföra sig som samma typ av allpassfilter med en reell pol och ett reellt nollställe speglat i den imaginära axeln (ekv. 4,8 och 12). Däremot var det bara 1:a ordningens filter som kunde lämna fasen opåverkad (ekv. 3). Ett allpassfilter har amplitudsvaret 1, men olinjär fasgång, fig 1. En effekt av detta är att fyrkanvågssvaret från ett allpassfilter är väldigt olikt en fyrkantvåg, fig 2. Eftersom vi såg i inledningen att det finns fördelar med branta filter är det intressant att utreda om ett sådant allpassfilter har någon hörbar påverkan på ljud. I elektroakustiklaborationen ”lyssningstest” lyssnar vi bla på ett sådant.

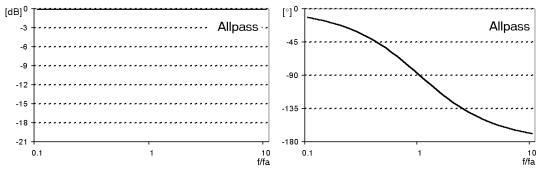
Fig 1. Amplitud- och fassvar för allpassfilter (ekv. 4, 8 och 12).

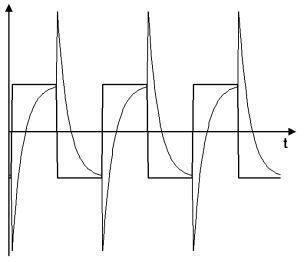
Fig 2. Fyrkantssvar för allpassfilter (ekv. 4, 8 och 12).

Andra dimensioneringar

I verkliga dimensioneringar ser man ofta olika ordningstal i högpass- och lågpassgrenarna. Sådana dimensioneringar ger nästan alltid en liten påverkan på frekvens- och fasgången. Påverkan är dock ofta mindre än andra effekter i högtalarsystemet och ibland kan man till och med dra nytta av den för att kompensera något annat. Även om påverkan för det mesta är hörbar, kan den vara liten jämfört med andra fördelar som erhålls. För den praktiska konstruktionen kan det alltså vara bättre att göra avsteg från teorin ovan, men förståelsen för resonemangen är ändå nyttiga att ha med sig när man gör den slutgiltiga dimensioneringen av delningsfiltret.

Vidare har vi endast behandlat tvåvägssystem, men teorin kan lätt utvidgas till att gälla flervägssystem genom att applicera fler filter.

Vi har heller inte tittat på möjligheten att göra digitala delningsfilter. Detta är en hel vetenskap i sig och här finns en hel mängd nya gropar att falla i.